גמטריה עברית ו/או גימטריה עיברית
מציאת קשרים מספריים בין מילים וביטויים. בין המסורות היהודיות הקדומות, קבוצה של יהודים מלומדים ספרה את ההופעות של האותיות בכתובים כמו כן גם את מס' המילים והביטויים מכאן הגיע שמם סופרים מלשון לספור. הסופרים הבטיחו כי כל מגילה בתורה וכל פרק הוא זהה ומדויק למקור. יש רבים הסבורים כי עזרא הסופר היה ממיסד קבוצה זו. בספר היצירה האותיות ואלף-בית מדומים לאבנים שמהם נבנה הבית. הן נקראות עשרים ושתיים אבני הבריאה. ישנה אמונה המצביעה על הקשר שבין האותיות והמילים לבין בריאת העולם. גימטריה היא שיטה לחישוב ערכם המספרי של אותיות מילים וביטויים וכמו כן משמשת לספירה. בעזרת גימטריה ניתן למצוא תובנות נוספות והקשרים חדשים שבין ביטויים. לפי כמה מקורות ישנן כמה שיטות שונות לחישוב הגימטריה. על פי ערך הגימטריה ניתן למצוא מילים וביטויים מקבילים שווי ערך גימטרי. להלן כמה משיטות חישוב הגימטריה השונות.
הסברים על הגמטריה העברית
גימטריה (כנראה, מיוונית: "גאמה טריה", גאמה = 3, או מ־"gematria" - "גאומטריה") היא מתן פרשנות למילה או למחרוזת מילים לפי סכום ערכן המספרי של האותיות. לאחר שהומרו למספרים, ניתן להשוות מילים זו לזו ולמצוא קווי דמיון. יש המייחסים למילים בעלות ערך מספרי זהה משמעות מיסטית, ויש הרואים בכך שעשוע.
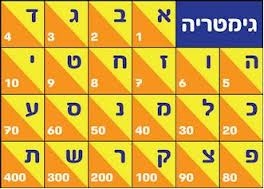
אותיות האלפבית העברי משמשות לכתיבת ספרות עבריות, לפי ערכן המספרי של האותיות המופיע בטבלה שמשמאל. לעתים יש ונותנים ערך נפרד לאותיות מנצפ"ך (כלומר האותיות הסופיות):
ך=500 ,ם=600 ,ן=700, ף=800, ץ=900.
דוגמאות
- "גימטריה": 3 + 10 + 40 + 9 + 200 + 10 + 5 = 277
- ההבדל בין רצוי (306) ל - מצוי (146) זה כסף (160)
- ההבדל בין שקר (600) ל - אמת (441) הוא קטן (159)
גימטריה בספרות התלמודית
הגימטריה כדרך לקבלת רמז להבנת הכתוב וככלי פרשני שולי נמצאת בשימוש בדברי התנאים ובתלמוד במדרש - באגדה בלבד, אך אין לומדים הלכות מגימטריה (אלא אם כן הן מקובלות במסורת כהלכה למשה מסיני). בברייתא של ר' אליעזר הגלילי היא נמנית עם המידות שהתורה נדרשת בהן באגדה. בפרקי אבות, לעומת זאת, מודגש ערכה השולי של הגימטריה: "ר' אליעזר בן חסמא אומר: קינין ופתחי נידה הן גופי הלכות, תקופות וגימטריאות - פרפראות לחכמה".
דוגמאות לגימטריה
* על הפסוק (בראשית יד, יד): "וישמע אברם, כי נשבה בן אחיו; וירק את חניכיו ילידי ביתו, שמונה עשר ושלש מאות, וירדוף, עד-דן" נאמר בברייתא כי 318 חניכיו ילידי ביתו אינם אלא אליעזר עבד אברהם לבדו, שהרי אליעזר = 318 בגימטריה. בפירושו לפסוק זה אברהם אבן עזרא מותח ביקורת על פרשנות זו ומציין: "וחשבון אותיות אליעזר דרך דרש, כי אין הכתוב מדבר בגימטריא, כי יכול יוכל הרוצה להוציא כל שם לטוב ולרע, רק השם כמשמעו".
* מהפסוק (במדבר, ו, ה): "עד מלאת הימים אשר יזיר לה', קדוש יהיה" נלמדת ההלכה (מסכת נזיר, ה/א) שנזירות שלא נקבע אורכה נמשכת 30 יום, כערכה של המילה "יהיה". הרא"ש, בפירושו שם, מזכיר את העובדה שפרט זה הוא הלכה למשה מסיני, ורק נסמך על הפסוק כרמז.
* הביטוי "נכנס יין יצא סוד" מופיע במסכת עירובין (דף סה/א) ושם מוסבר כי בנוסף להשפעתו המשחררת לשון של היין, תכונה זו שלו נרמזת גם בגימטריה: יין = 70 = סוד.
שימוש בגימטריה נעשה גם בספרות רבנית בתר-תלמודית, ולהלן דוגמאות אחדות:
* על דברי יעקב אבינו: "עם לבן גרתי" (בראשית, לב, ה) אומר רש"י: "גרתי בגימטריא תרי"ג, כלומר עם לבן הרשע גרתי ותרי"ג מצוות שמרתי". פירוש זה מיוחס לרבי משה הדרשן.
* על דברי אחשוורוש להמן במגילת אסתר: "הכסף נתון לך והעם לעשות בו כטוב בעיניך", מפרשים התוספות (מסכת מגילה יג/ב): "גימטריא דהכסף עולה הע"ץ, רמז לו שיתלה עליו" (כלומר הכסף = 165 = העץ).
הרמב"ן פעל לצמצום השימוש בגימטריה ככלי לפרשנות, וקבע "אין אדם רשאי לדון בחשבון גימטריות ולהוציא מהן עניין עלה בדעתו". בספר "בעל הטורים" של רבי יעקב בן אשר נעשה שימוש נרחב בגימטריה. המחבר מתאר פרשנות זו כ"מעט פרפראות וגימטריות וטעמי המסורות, להמשיך הלב" והיא משמשת כמבוא לפרשנותו המקיפה לתורה. גם המהר"ל מפראג ופרשנים חסידיים השתמשו בגימטריה.
גימטריה בקבלה
השימוש בגימטריה כחלק מהקבלה החל להתפתח בהמאה ה-12 ואילך, בהתאם לגישה שהעולם נברא באמצעות צירופים שונים של האלפבית העברי. הגימטריה שימשה כדרך להביא אסמכתא נוספת לחיזוקו של רעיון שיש לו מקורות אחרים, וכאמצעי עזר לזיכרון. שימוש נרחב בגימטריה כדרך לפענח את הכוונות הנסתרות שבתפילה וככלי לפרשנות המקרא מופיע בכתביהם של רבי אלעזר מוורמס ותלמידיו. שימוש נרחב ביותר בגימטריה מופיע בכתביו של רבי אברהם אבולעפיה.
גרשם שלום, חוקר הקבלה הנודע, מציין: "בהמשך התפתחות הקבלה מצטיירות שתי מגמות: של חובבי הגימטריה ושל הממעטים להשתמש בה. בדרך כלל ניתן לומר, שרעיונות חדשים נתפתחו תמיד מעבר לתחום הגימטריה, אולם תמיד נמצאו חכמים שמצאו להם ביסוסים או הקשרים רחבים בדרך הגימטריה, ובלי ספק ייחסו להם ערך ממשי העולה על זה של אסמכתא בעלמא" (האנציקלופדיה העברית, כרך י', עמ' 686).
במאה ה-17 יצא לאור הספר "מגלה עמוקות" של נתן שפירא ובו שימוש נרחב ומעמיק בגימטריה כדרך להגות ולפרשנות. לספר זה הייתה השפעה ניכרת על הבאים אחריו. השבתאים השתמשו בגימטריה כדי להוכיח את משיחיותו של שבתי צבי, ומתנגדיהם השתמשו בטכניקה זו כדי להוכיח את ההיפך (למשל באמצעות הגימטריה שבתי צבי = 814 = רוח שקר).
גימטריה בימינו
יש פרשנים המשתמשים בגימטריה ככלי להבנה והארה של מושגים וטקסטים, כך למשל אחד = 13 = אהבה, או אשה = 306 = דבש. למעשה, עבור רוב הקשרים-לכאורה המוצגים בעזרת גימטריה ניתן למצוא גם קשרים הפוכים לגמרי, פירושים סותרים לאותם צירופי אותיות. למשל כתוב בפרשת בהעלותך שמרים מדברת אודות ציפורה, אשת משה, ואומרת שהיא "אישה כושית". רש"י מפרש "מגיד שהכל מודים ביופיה, כשם שהכל מודים בשחוריתו של כושי", ומחזק את דבריו באומרו "כושית בגימטריה יפת מראה". בדיקה מראה כי כושית בגימטריה גם מכוערת. שימוש הומוריסטי בגימטריה נעשה בתוכנית הטלוויזיה "זהו זה", שבה הופיעה דמותו של הבבא בובה, פרודיה על דמותו של מקובל, המשתמש בגימטריה למתן פרשנות לאירועים אקטואליים.
שיטות גימטריה נוספות
בנוסף לשיטת הגימטריה הבסיסית, שבה ניתן לכל אות ערך מספרי, התפתחו שיטות גימטריה נוספות, המאפשרות להגיע לשוויונות שאינם נוצרים בשיטה הבסיסית. אחדות מהן מופיעות בספרו של משה קורדובירו, "פרדס רימונים", ובהן:
- מספר מעוגל, שאינו מביא בחשבון את האפסים בעשרות ובמאות, ולכן, למשל, ל = 3, ק = 1.
- מספר מרובע, שבצד אחד של המשוואה נלקחים ערכים הריבועים של מספרי האותיות. דוגמה: דוד = 42 + 62 + 42 = 68 = חכם.
- מספר קדמי, שבו ערכה של אות שווה לסכום ערכי כל האותיות החל מהאות א ועד לאות הנתונה. דוגמה: ג = 1 + 2 + 3 = 6.
דוגמה נוספת: כ = 10+20+... +1+2+3 = 75 - מילוי: ערכה של אות שווה לערך השם המלא של האות. ערכה של ח, למשל, שווה לזה של "חית", כלומר 418.
- הכולל: הוספת מספר האותיות שבמילה לערכה של המילה, או הוספת 1 לערכה של המילה.
גימטריה קטנה
צורה נפוצה פחות של שימוש בגימטריה נקראת גימטריה קטנה. בגימטריה קטנה, מחשבים את הערך הגימטרי של מילה, צירוף מילים או משפט על פי סכום ערכי האותיות המרכיבות אותו, ואחר-כך מסכמים את הספרות של הסכום שוב ושוב עד לקבלת מספר מ-1 עד 9. או אז, מתייחסים למספר זה כאל ערכו הגימטרי של המילה/צירוף המילים/המשפט האמור. הדבר שקול לגימטריה מודולו 9. לעוסקים בנומרולוגיה מאפשרת הגימטריה הקטנה לקשר בין הערך הגימטרי של המילים לבין המשמעות הנומרולוגית של התוצאה. השימוש הנפוץ בגימטריה, אשר בו לא מסכמים את ספרות התוצאה, נקרא בהתאמה, גימטריה גדולה.
גימטריה בערבית
במהלך ימי הביניים אימצו אנשי דת מוסלמים את הגימטריה מן היהודים כשיטה לפירוש הקוראן, והתאימו אותה לאלפבית הערבי. אנשי הדת המוסלמים הצמידו לכל אות ערבית את הערך שניתן למקבילתה האטימולוגית בעברית. כך, האות הערבית ? קיבלה את הערך 1 (מקבילה ל-א), ? קיבלה את הערך 2 (מקבילה ל-ב), ? -3 (ג), ? -4 (ד) וכן הלאה. סדר האותיות המקובל בערבית שונה במידה ניכרת מהמקובל בעברית, ולפיכך, בניגוד לעברית, אין התאמה בין סידור האותיות המשמש במילונאות הערבית, לבין סידור האותיות הערביות על-פי ערכן בגימטריה. לדוגמה, ארבע האותיות הראשונות באלפבית הערבי הן ? ? ? ?, אך אם נסדר את האותיות הערביות על פי ערכן בגימטריה, יהיו ארבע האותיות הראשונות: ? ? ? ? , ואילו ? תבוא לקראת סוף הרשימה, כיוון שהיא מקבילה ל-ת בעברית, וערכה 400. כיוון שבאלפבית הערבי יש 28 אותיות, הגימטריה הערבית אינה עוצרת ב-400, ויש בה אותיות שערכן גבוה יותר. בנוסף, מקובל לתת ערך מספרי לליגטורה ?? (צירוף של האותיות ? ו-?).
השיטה הרגילה
עבור כל אות ישנו ערך מספרי ויש לחבר בין הערכים בכדי לקבל את התוצאה בגימטריה.

לדוגמא:
המילה שלום: 40 + 6 + 30 + 300 = 376
מוספי:
במספר מוספי מוספים את מס' האותיות במילה לערך המתקבל:
שלום = 300 + 30 + 6 + 40 + 4 = 380
מספר גדול
דומה לשיטה הרגילה אך האותיות הסופיות ממשיכות את הסדר של המספרים

לדוגמא: המילה שלום: ש + ל + ו + ם = 300+30+6+600 = 936
מספר קטן
בשיטה זו, אין משמעות לכפולות עשרוניות, כלומר כל אות שווה לספרה הבודדת
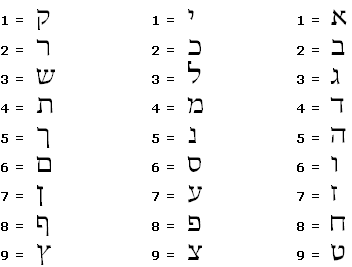
![]()
לדוגמא: שלום = 3+3+6+6 = 18
סדרתי
על פי שיטה זו האותיות מקבלות את הערך הרץ הסדרתי שלהן
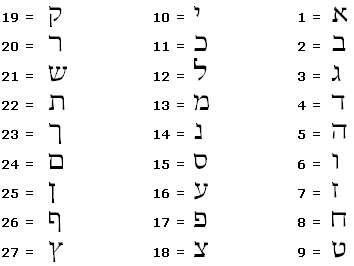
לדוגמא: שלום = 21+12+6+24 = 63
את בש
השיטה ההופכית, בא כל אות מקבלת את הערך של האות הנגדית לה מהסוף להתחלה
שימו לב כי את בש, נותן את אותו הערך גם בשיטה הרגילה וגם בשיטת את בש.

לדוגמא: שלום = 2+20+80+10 = 112
מספר קידמי
בשיטה זו כל אות מקבלת את הערך של סכום הערכים של האותיות עד אליה כולל.
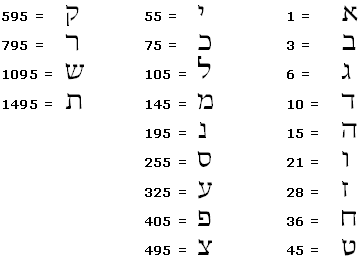
לדוגמא: שלום = 1095+105+21+145 = 1366
מספר פרטי
כל אות מקבלת את הערך של האות בריבוע הגימטרי

לדוגמא: שלום = 90000+900+36+1600 = 92536
מספר שמי
ערך כל אות שווה לערך הגימטרי של השם המלא של האות
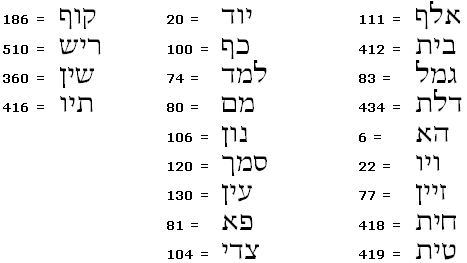
לדוגמא: שלום = 360+74+22+80 = 535
נושאים נוספים בגימטריה
- גימטריא
- גימטריה התאמה
- שמות לתינוק בגימטריה ובנומרולוגיה
- יהוא
- גימטריה עיברית
- חידות בגימטריה באנגלית
- משמעות שמות גימטריה
- גימטריה ברכה
- גימטריה חוקים
- מתרגם גימטריה
- מילון גימטריה
- בחירת שמות גימטריה
- שמות ילדים גימטריה
- גימטריה המספר
- גימטריה ברכות
- גימטריה מספרים
- האפס בגימטריה
- בחירת שם גימטריה
- פרושי גימטריה
- גימטריה של השם יהוא
- גימטריה פירוש
- מילים בגימטריה
- גימטריה פירושים
- פירוש גימטריה
- גימטריה חתונה
- מילים גימטריה
- גימטריה תרגילים
- מציאת שמות גימטריה
- משמעות גימטריה
- גימטריה מילים
- גימטריה זוגיות
- פירוש שמות גימטריה
- גימטריה חידות
- גימטריה לשמות אנשים
- חידות גימטריה והגיון
- גימטריה מרים
- גימטריה שמות של בנות
- פרוש שמות לפי גימטריה
- תוכנה לגימטריה
- גימטריה 68 במילים
- תוכנה לחישוב גימטריה
- פירושי גימטריה
- גימטריה שמות ילדים
- שמות בנות גימטריה
- שישים לפי גימטריה
- גימטריה שם ע
- גימטריה יאיר
- תכנה לגימטריה
- משחקי גימטריה
- שמות לתינוק גימטריה
- גימטריה תרגילי מילים
- רשימת הגימטריה
- גימטריה לבדיקת התאמה זוגית
- גימטריה לשמות
- רשימת שמות גימטריה
- חידות גימטריה
- אנימציה גימטריה
- גימטריה בקבלה
- לימוד גימטריה
- בגימטריה ביטויים
- גימטריה שמות חיפוש
- הקבלה גימטריה זוגיות
- גימטריה של שמות
- קתרינה גימטריה
- גימטריה שמות
- שבת גימטריה
- שם לפי גימטריה
- התאמה זוגית גימטריה
- גימטריה שישים
- פירוש שמות בגימטריה
- גימטריה אקסל
- גימטריה הפוכה
- גימטריה 576
- גימטריה לפי שם




